Au 17e siecle, l'apparition des logarithmes va permettre aux astronomes et aux navigateurs d'effectuer des calculs plus efficaces en trigonomérie plane et sphérique. Ces derniers avaient surtout besoin de tables de valeurs de logarithme de sinus log(sin(x)). C'est pourquoi les premières tables étaient conçues pour cela.
Bien entendu, tous les calculs au 17e, 18e, 19e se faisaient à la main (papier, crayon). Et même au début du 20e, les calculatrices élecroniques et ordinateurs n'existant pas, au mieux, on disposait de calculatrices mécaniques ne faisant que des additions et soustractions à 10 chiffres au plus.
Techniciens, lycéens et étudiants, dans les années 60/70, ne disposaient souvent que d'une tables de logarithmes, de papier/crayons et d'une Règle à Calcul". Cette dernière, s'appuyant sur les échelles logarithmiques permettait d'effectuer des produits et quotients avec une précision de 0.2% en moyenne. Les tables de logarithmes, elles, permettaient d'atteindre des précision de 10-7.
Parlons de la précision précision des tables. Celle-ci s'exprime par le nombre de chiffres significatifs en sortie (on parle encore de nombre des décimales ou de nombre de place). Par exemple, les tables Bouvart & Ratinet destinées aux étudiants et lycéens, au début du 2Oe, permettaient à partir d'un nombre de 4 chiffres significatifs d'obtenir un logarithme à 5 décimales (chiffres significatifs) (voir 6 décimales par interpolation). Plus le nombre de places des entrées est important, plus l'ouvrage est volumineux.
Attention ! Dans ce qui suit, on ne traitera que les logarithmes en base 10 (dits décimaux). Donc \( \boxed{\log \equiv \mbox{Log}_{10} \equiv \log_{10}} \)
Exemple :
Soit \(x = 3245\), un nombre doté de 4 chiffres significatifs.
Pour calculer \(\log_{10}(3245)\), posons \(x=3.245 \times 10^3 \), alors \(\log_{10} x = 3 + \log_{10}(3.245)\approx 3 + 0,51121 \).
Je profite de cette page pour présenter un compagnon de calcul, la table de logarithmes ""BOUVART & RATINET". Très répendue en France, elle permettait à ma génération d'étudiant d'améliorer la précision des opérations s'appuyant sur les propriétés des logarithmes. Elles existaient en 2 couleurs
- Rouge : avec un supplément d'une quarantaine de pages, contenant des formules usuelles de mathématiques, physique et chimie (non autorisée aux examens)
- Jaune : sans le supplément (autorisée aux examens)
USAGE DES TABLES DE LOGARITHMES BOUVART & RATINET
Quelques rappels :
Pour utiliser les "Tables de logaritmes", le nombre N dont on cherche le logarithme doit d'abord être réécrit comme suit :
Donc \(\log(N)= \log(10^c)+\log(x)=c+\log(x)\)
2 exemples de réécriture (j'emploie le terme de normalisation),
- sa partie entière appelée caractéristique \(c\)
- sa partie décimale appelée mantisse \(m=\log(x)\)
$$ \left . \underbrace{ 1 }_{caractéristique\ c} \overbrace{.511307037449982...}^{mantisse\ m} \right . $$
Les Tables de logarithmes "Bouvart & Ratinet" (notées Table de logarithmes B&R) donnent une valeur des logarithmes pour des nombres N ayant jusque 4 chiffres significatifs.
Il est possible d'aller jusque 5 chiffres en entrée en appliquant une interpolation linéaire entre 2 encadrants. La précision de la mantisse est de 5 chiffres significatifs
Il existe des tables (volumineuses) admettant 5 (6 en interpolant) chiffres significatifs et 7 chiffres pour la mantisse.
Calculons le logarithme de 32.4569
On commence par normaliser 32.4569
\(32.4569 = 3.24569 \times 10^1 \Longrightarrow \log(32.4569)=1+\log(3.24569)\). Sa caractéristique \(c\) sera donc 1. Il reste à trouver sa mantisse \(m=\log(3.24569)\) .
Notre table n'admet que 4 chiffres significatifs. On peut donc poser \( 3.245 < 3.24569 < 3.246\)
Cherchons, dans notre (extrait de) Tables de logarithmes B&R les entrées 3245 et 3246 sans se préoccuper du point décimal.
- Pour 3.245, on trouve 51121. Ce qui signifie que \(\log(3.245)\approx 0.51121\)
- Pour 3.246, on trouve 51135. Ce qui signifie que \(\log(3.246)\approx0.51135\)
Reportons ces valeurs dans un tableau pour y voir plus clair.
| Tbl. | log | Tbl. |
|---|---|---|
| 3245 | 0.51121 | 51121 |
| 3246 | 0.51135 | 51135 |
| ∆=1 | ∆=14 | |
On note que la différence entre 51135 et 51121 est 14. Dans notre (extrait de) table, on observe un petit tableau en haut à gauche numéroté 14.
Revenons à N = 32.45(69) et isolons les chiffres au delà de 3245. C'est dire 69; formé de 6 et 9.
Dans le tableau [14],
| en face de 6 on trouve | 8.4 | soit | 8.4 x 10-5 |
| en face de 9 on trouve | 12.6 | soit | 1.26 x 10-5 |
| Somme | 9.66 x 10-5 | ||
Comparons ce résultat à ceux donnés par une calculatrice et une règle à calcul
| Calculatrice | 1.51130704... | |
| Table | 1.5113066 | |
| Erreur | 0.00000044 | |
| Err. relat. | 2.9 10-7 |
On est bien loin du pauvre résultat obtenu avec une règle à calcul
| Calculatrice | 1.51130704... | |
| Règle | 1.51 | |
| Erreur | 0.0013 | |
| Err. relat. | 8.6 10-4 ≈10-3 |
Voyons ce que donne une interpolation linéaire pour passer de \(\log(3.245)\) à \(\log(3.24569)\)
En fait, on peut éviter cette méthode et donc des multiplications/divisions, grace aux petits tableaux placés dans les marges à gauche ou à droite. Seules des additions/soustractions sont nécessaires.
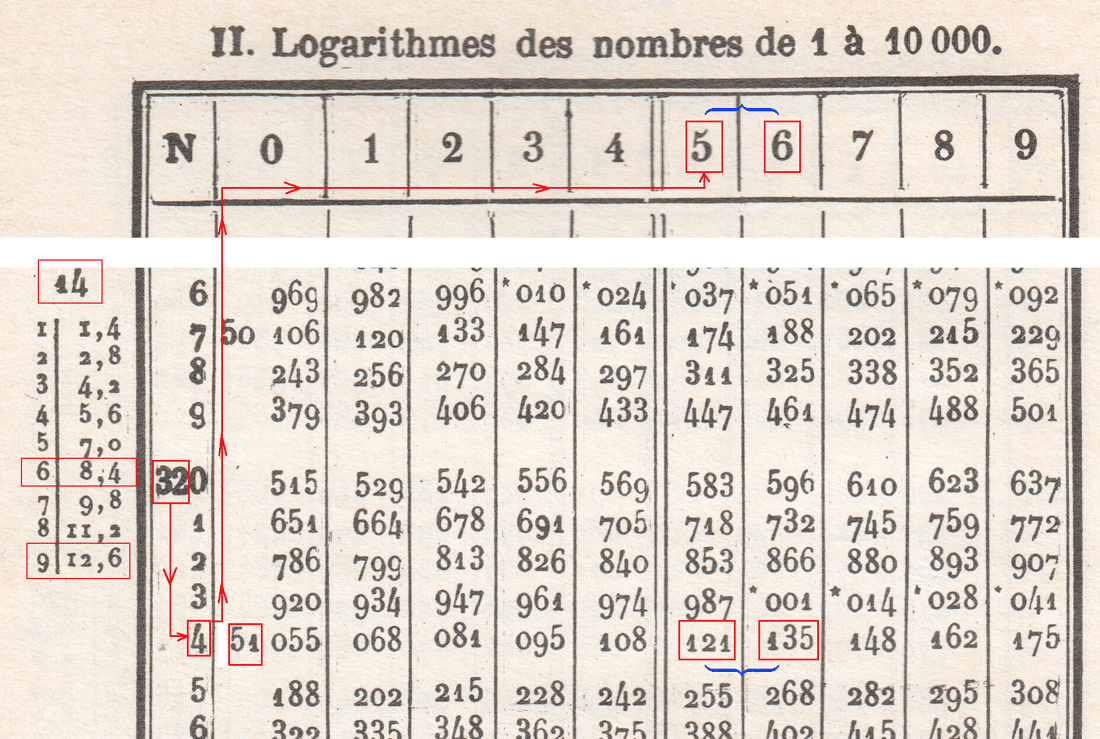Extrait de la Tables de logarithmes B&R (page 8)
Les Tables de logarithmes contiennent aussi des log de sinus et cosinus. Hors la notation utilisée peut surprendre. Prennons un exemple.
Déterminons log(sin 30°)
\(\sin 30° =0.5 <1 \Longrightarrow\) son logarithme sera donc négatif.
Dans la table B&R en page 12, on cherche l'entrée 5000 (pour 0.5000). En regard, on peut lire \(69 897\). Donc \(\log(\sin 30°) \approx -1 + 0.69897 \approx -0,30103 \).
Passons maintenant à la page 170 qui donne directement \(\log(\sin 30°)\). On trouve \(\log(\sin 30°) \approx \overline{1}.69897\). Cette drôle de notation permet d'inscrire des valeurs négatives de log de façon compacte. Pour résumer,
(dans les tables Bouvart & Ratinet)
Dans d'autres tables, les anglo-saxonnes ou celles datant d'avant le 20e siècle, on trouve une autre notation pour les valeurs négatives de logarithme.
(dans les tables anglo-saxonnes)
\(\sin(30°)=0.5 <1 \Longrightarrow\) son logarithme sera donc négatif. Dans la table B&R, on cherche l'entrée 5000 (pour 0.5000 en page 12). On peut lire \(69 897\). Donc \(\log(\sin(30°)) \approx -1 + 0.69897 \approx -0,30103 \).
Passons maintenant à la page 170 qui donne directement \(\log(\sin(30°))\). On trouve \(\log(\sin(30°)) \approx \overline{1}.69897\). Cette drôle de notation permet d'inscrire des valeurs négatives de log.
Pour résumer, \( \boxed{\log(\sin(30°)) \approx \overline{1}.69897 \approx -1 + 0.69897 \approx -0,30103}\)
