La détermination de l'inductance d'une bobine peut être nécessaire pour la
restauration des TSF ou pour la compréhension de sa conception. Il n'existe pas de formules
analytiques donnant la valeur exacte de l'inductance. C’est pourquoi au début du 20ème
siècle, les premiers outils de calculs approchés basés sur des tables ou des formules empiriques
ont vu le jour et donnaient des résultats satisfaisants pour les besoins courants. L'arrivée des
calculateurs numériques a permis la détermination rapide, précise et adaptée aux formes des
bobinages les plus différentes de l'inductance mutuelle et donc de la self-inductance.
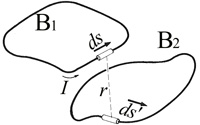
fig.1 2 boucles
Une boucle \(B1\) de courant \(i_1\) crée un flux qui la traverse. Si elle est a proximité d'une autre
boucle \(B2\), une partie du flux \(\phi_1\) traverse \(B2\). Apparait alors un courant \(i_2\) qui
dépend de \(i_1\), de la distance \(r\) entre les boucles, de leurs formes, ..
Ce courant \(i_2\) crée un flux \(\phi_2\). Une partie du flux \(\phi_2\) traverse la première boucle \(B1\). Donc celle-ci est traversée par 2 flux \(\phi_1\) et \(\phi_2\). Le flux \(\phi_1\) dépend de l'inductance propre \(L1\) de la boucle B1 et la portion de flux issu de la boucle \(B2\) dépend de l'inductance \(L2\) mais aussi de la forme est de l'éloignement de cette seconde boucle. On introduit alors un coefficient \(M_{12}\) appelé inductance mutuelle.
Deux boucles en série très éloignées présentent une inductance qui est la somme des inductances propres à chaque boucle. Lorsque les boucles sont proches, l'interaction entre elles fait intervenir l'inductance mutuelle.
Ce courant \(i_2\) crée un flux \(\phi_2\). Une partie du flux \(\phi_2\) traverse la première boucle \(B1\). Donc celle-ci est traversée par 2 flux \(\phi_1\) et \(\phi_2\). Le flux \(\phi_1\) dépend de l'inductance propre \(L1\) de la boucle B1 et la portion de flux issu de la boucle \(B2\) dépend de l'inductance \(L2\) mais aussi de la forme est de l'éloignement de cette seconde boucle. On introduit alors un coefficient \(M_{12}\) appelé inductance mutuelle.
Deux boucles en série très éloignées présentent une inductance qui est la somme des inductances propres à chaque boucle. Lorsque les boucles sont proches, l'interaction entre elles fait intervenir l'inductance mutuelle.
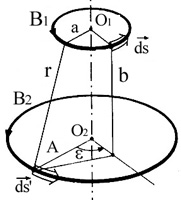
fig.2 2 boucles coaxiales
la formule de Neumann
L’inductance mutuelle peut être calculée à l’aide de la formule de Neumann.\(\displaystyle M=\frac {\mu_0}{4\pi} \iint \frac {\overrightarrow {ds} \overrightarrow {ds'}}{r} \)
Ici \(ds\) et \(ds'\) sont des vecteurs segments élémentaires des boucles et r est la distance qui les séparent. \(a\) et \(A\) sont les rayons des boucles coaxiales occupant 2 plans parallèles distants de \(b\).
\(\displaystyle M_{12}=\frac {\mu_0}{4\pi} \iint \frac {\cos \epsilon}{r} \)
Par exemple, dans le cas dans le cas de 2 spires coaxiales et placées dans 2 plans parallèles la formule de Neumann peut s’écrire comme suit.
Cette intégrale classique peut écrite en passant par 2 intégrales elliptiques.
$$\begin{cases} r=\sqrt{A^2+a^2+b^2-2Aa\cos {(\varphi-\varphi')}}\\ \epsilon=\varphi - \varphi' \mbox{ , } ds=ad\varphi \mbox{ , } ds'=Ad\varphi' \end{cases} $$
Encore une fois, en s'appuyant sur l'hypothèse de spires concentriques, on peut écrire la distance \(r\) qui sépare les 2 éléments \(ds\) et \(ds'\) en fonctions des rayons respectifs \(a\), \(A\) et l'angle \(\epsilon\) .
En effectuant les changements de variables d'intégration ci-contre, on peut écrire la formule de Neumann sont la forme donnée ci-dessous. $$\displaystyle M_{12}=\frac {\mu_0}{4\pi}\int_0^{2\pi}\!\!\!\!\!\int_0^{2\pi}\frac{Aa\cos {(\varphi-\varphi')}d\varphi d\varphi'}{\sqrt{A^2+a^2+b^2-2Aa\cos {(\varphi-\varphi')}}}$$ Cette intégrale classique peut être exprimée en passant par les fonctions \(K\) et \(E\).
\(K\) et \(E\) sont des intégrales elliptiques complètes respectivement de première et seconde espèce.
$$\displaystyle M_{12}=-\mu_0\sqrt{Aa}\left\lbrack(k-\frac{2}{k})K+-\frac{2}{k}E\right\rbrack\frac{}{} \mbox{ ; }k=\frac{2\sqrt{Aa}}{\sqrt{(A+a)^2+b^2}}$$
A ce stade, \(M_{12}\) a encore une forme non approchée. On introduit une variable \(k\). Il reste à determiner \(K\) et \(E\)
\(K\) est une intégrale elliptique complète de première espèce $$\displaystyle K=F(k,\pi/2)=F(k)=\int_0^{\pi/2}\frac{d\varphi}{\sqrt{1-k^2\sin^2\varphi}d\varphi}$$ \(E\) est une intégrale elliptique complète de seconde espèce $$\displaystyle E=E(k,\pi/2)=E(k)=\int_0^{\pi/2}\sqrt{1-k^2\sin^2\varphi}d\varphi$$
Dans le cas d'une bobines composée de \(n\) spires et en appliquant le principe de superposition, on peut sommer les Mij comme montré ci-contre. Le nombre de termes de la somme n'est pas en \(n^2\) mais en \(2^n - 1\). $$\displaystyle M_{total}=\sum_{i=1}^{n_1}\sum_{j=1}^{n_1}M_{ij}$$
$$\begin{cases} r=\sqrt{A^2+a^2+b^2-2Aa\cos {(\varphi-\varphi')}}\\ \epsilon=\varphi - \varphi' \mbox{ , } ds=ad\varphi \mbox{ , } ds'=Ad\varphi' \end{cases} $$
Encore une fois, en s'appuyant sur l'hypothèse de spires concentriques, on peut écrire la distance \(r\) qui sépare les 2 éléments \(ds\) et \(ds'\) en fonctions des rayons respectifs \(a\), \(A\) et l'angle \(\epsilon\) .
En effectuant les changements de variables d'intégration ci-contre, on peut écrire la formule de Neumann sont la forme donnée ci-dessous. $$\displaystyle M_{12}=\frac {\mu_0}{4\pi}\int_0^{2\pi}\!\!\!\!\!\int_0^{2\pi}\frac{Aa\cos {(\varphi-\varphi')}d\varphi d\varphi'}{\sqrt{A^2+a^2+b^2-2Aa\cos {(\varphi-\varphi')}}}$$ Cette intégrale classique peut être exprimée en passant par les fonctions \(K\) et \(E\).
\(K\) et \(E\) sont des intégrales elliptiques complètes respectivement de première et seconde espèce.
$$\displaystyle M_{12}=-\mu_0\sqrt{Aa}\left\lbrack(k-\frac{2}{k})K+-\frac{2}{k}E\right\rbrack\frac{}{} \mbox{ ; }k=\frac{2\sqrt{Aa}}{\sqrt{(A+a)^2+b^2}}$$
A ce stade, \(M_{12}\) a encore une forme non approchée. On introduit une variable \(k\). Il reste à determiner \(K\) et \(E\)
\(K\) est une intégrale elliptique complète de première espèce $$\displaystyle K=F(k,\pi/2)=F(k)=\int_0^{\pi/2}\frac{d\varphi}{\sqrt{1-k^2\sin^2\varphi}d\varphi}$$ \(E\) est une intégrale elliptique complète de seconde espèce $$\displaystyle E=E(k,\pi/2)=E(k)=\int_0^{\pi/2}\sqrt{1-k^2\sin^2\varphi}d\varphi$$
Dans le cas d'une bobines composée de \(n\) spires et en appliquant le principe de superposition, on peut sommer les Mij comme montré ci-contre. Le nombre de termes de la somme n'est pas en \(n^2\) mais en \(2^n - 1\). $$\displaystyle M_{total}=\sum_{i=1}^{n_1}\sum_{j=1}^{n_1}M_{ij}$$
