Bobines monocouche
(Joseph-Henri Lévy)
La détermination de l'inductance d'une bobine peut être nécessaire pour
la restauration des TSF ou pour la compréhension de sa conception.
Il n'existe pas de formules analytiques donnant la valeur exacte de l'inductance.
C'est pourquoi au début du 20ème siècle, les premiers outils de
calculs approchés basés sur des tables ou des formules empiriques ont vu
le jour et donnaient des résultats satisfaisants pour les besoins courants.
La seule formule de calcul de l'inductance d'une bobine, sous forme analytique, s'applique à un solénoïde de longueur \(l\) « quasi-infinie », de diamètre \(D\) et de densité linéique de spires \(n\) (voir Eq.1). Elle peut prendre la forme : $$L(µH)=\frac{ (\pi n D)^2 }{1000} l \quad \quad \quad (1)$$ Les spires peuvent être jointives ou non. \(D\) et \(n\) sont en unités CGS, donc en centimètres. La relation (1) donne \(L\) en micro-Henrys (µH).
La seule formule de calcul de l'inductance d'une bobine, sous forme analytique, s'applique à un solénoïde de longueur \(l\) « quasi-infinie », de diamètre \(D\) et de densité linéique de spires \(n\) (voir Eq.1). Elle peut prendre la forme : $$L(µH)=\frac{ (\pi n D)^2 }{1000} l \quad \quad \quad (1)$$ Les spires peuvent être jointives ou non. \(D\) et \(n\) sont en unités CGS, donc en centimètres. La relation (1) donne \(L\) en micro-Henrys (µH).
une méthode tabulaire - formule de Nagaoka

fig.1 Hontaro Nagaoka
Dans le cas d'une longueur finie,
quelques millimètres ou centimètres pour les TSF, des formules de calculs approchés peuvent
prendre la forme :
$$L(µH)=K \frac{ (\pi n D)^2 }{1000} l \quad \quad \quad \quad (2)$$
Le paramètre \(K\) dépend de la «
géométrie » de la bobine exprimée par le rapport \(D/l\). Le savant japonais Hontaro
Nagaoka a publié au début du XXème siècle une table permettant
de déterminer \(K\) en fonction du rapport \(D/l\).
Une autre formule plus pratique d'utilisation et de même précision utilise une constante \(K1\) dérivée de \(K\). Elle dépend de la même façon de du rapport \(D/l\). $$L(µH)=K_1 \frac{N^2 D}{100} \quad \quad \quad \quad (3)$$ Un exemple de calcul ici :
Une autre formule plus pratique d'utilisation et de même précision utilise une constante \(K1\) dérivée de \(K\). Elle dépend de la même façon de du rapport \(D/l\). $$L(µH)=K_1 \frac{N^2 D}{100} \quad \quad \quad \quad (3)$$ Un exemple de calcul ici :
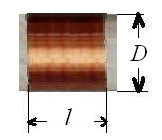
fig.2 Bobine
Exemple :
Calculons l'inductance L d'une bobine de 100 spires jointives bobinées sur un mandrin de
soit L ≈ 177 µH .
Cette valeur et les dimensions de la bobine correspondent aux bobines d'accord rencontrées dans la gamme des petites ondes (PO).
- diamètre D = 2,6 cm
- longueur l = 2,6 cm
soit L ≈ 177 µH .
Cette valeur et les dimensions de la bobine correspondent aux bobines d'accord rencontrées dans la gamme des petites ondes (PO).
Pour information \(K_1\) est déduit de \(K\) par la relation : \( \displaystyle K_1 = \frac{\pi^2}{10}(\frac{D}{l}) K_{(D/l)}\) avec \(D\) et \(l\) en centimètres.
Une table des coefficients de Nagaoka
| D/l | K | K1 |
|---|---|---|
| 0.00 | 1.00000 | 0.00000 |
| 0.01 | 0.99577 | 0.00983 |
| 0.02 | 0.99156 | 0.01957 |
| 0.03 | 0.98738 | 0.02924 |
| 0.04 | 0.98322 | 0.03882 |
| 0.05 | 0.97909 | 0.04832 |
| 0.06 | 0.97499 | 0.05774 |
| 0.07 | 0.97090 | 0.06708 |
| 0.08 | 0.96685 | 0.07634 |
| 0.09 | 0.96281 | 0.08552 |
| 0.10 | 0.95881 | 0.09463 |
| 0.11 | 0.95482 | 0.10366 |
| 0.12 | 0.95087 | 0.11262 |
| 0.13 | 0.94693 | 0.12150 |
| 0.14 | 0.94303 | 0.13030 |
| 0.15 | 0.93914 | 0.13903 |
| 0.16 | 0.93528 | 0.14769 |
| 0.17 | 0.93145 | 0.15628 |
| 0.18 | 0.92764 | 0.16480 |
| 0.19 | 0.92385 | 0.17324 |
| 0.20 | 0.92009 | 0.18162 |
| 0.21 | 0.91636 | 0.18993 |
| 0.22 | 0.91264 | 0.19816 |
| 0.23 | 0.90895 | 0.20633 |
| 0.24 | 0.90529 | 0.21444 |
| D/l | K | K1 |
|---|---|---|
| 0.25 | 0.90165 | 0.22247 |
| 0.26 | 0.89803 | 0.23044 |
| 0.27 | 0.89444 | 0.23835 |
| 0.28 | 0.89087 | 0.24619 |
| 0.29 | 0.88732 | 0.25397 |
| 0.30 | 0.88380 | 0.26168 |
| 0.31 | 0.88030 | 0.26934 |
| 0.32 | 0.87683 | 0.27693 |
| 0.33 | 0.87338 | 0.28446 |
| 0.34 | 0.86995 | 0.29193 |
| 0.35 | 0.86654 | 0.29933 |
| 0.36 | 0.86316 | 0.30669 |
| 0.37 | 0.85980 | 0.31398 |
| 0.38 | 0.85646 | 0.32121 |
| 0.39 | 0.85315 | 0.32839 |
| 0.40 | 0.84985 | 0.33551 |
| 0.41 | 0.84658 | 0.34257 |
| 0.42 | 0.84334 | 0.34958 |
| 0.43 | 0.84011 | 0.35654 |
| 0.44 | 0.83691 | 0.36344 |
| 0.45 | 0.83372 | 0.37028 |
| 0.46 | 0.83056 | 0.37708 |
| 0.47 | 0.82742 | 0.38382 |
| 0.48 | 0.82431 | 0.39051 |
| 0.49 | 0.82121 | 0.39715 |
| D/l | K | K1 |
|---|---|---|
| 0.50 | 0.81814 | 0.40373 |
| 0.51 | 0.81508 | 0.41027 |
| 0.52 | 0.81205 | 0.41676 |
| 0.53 | 0.80904 | 0.42320 |
| 0.54 | 0.80605 | 0.42959 |
| 0.55 | 0.80308 | 0.43593 |
| 0.56 | 0.80012 | 0.44223 |
| 0.57 | 0.79719 | 0.44848 |
| 0.58 | 0.79428 | 0.45468 |
| 0.59 | 0.79139 | 0.46083 |
| 0.60 | 0.78852 | 0.46695 |
| 0.61 | 0.78567 | 0.47301 |
| 0.62 | 0.78284 | 0.47903 |
| 0.63 | 0.78003 | 0.48501 |
| 0.64 | 0.77724 | 0.49095 |
| 0.65 | 0.77447 | 0.49684 |
| 0.66 | 0.77171 | 0.50269 |
| 0.67 | 0.76898 | 0.50850 |
| 0.68 | 0.76626 | 0.51426 |
| 0.69 | 0.76356 | 0.51999 |
| 0.70 | 0.76089 | 0.52567 |
| 0.71 | 0.75822 | 0.53132 |
| 0.72 | 0.75558 | 0.53693 |
| 0.73 | 0.75296 | 0.54249 |
| 0.74 | 0.75035 | 0.54802 |
| D/l | K | K1 |
|---|---|---|
| 0.75 | 0.74776 | 0.55351 |
| 0.76 | 0.74519 | 0.55896 |
| 0.77 | 0.74264 | 0.56437 |
| 0.78 | 0.74010 | 0.56975 |
| 0.79 | 0.73758 | 0.57509 |
| 0.80 | 0.73508 | 0.58040 |
| 0.81 | 0.73259 | 0.58566 |
| 0.82 | 0.73013 | 0.59090 |
| 0.83 | 0.72767 | 0.59609 |
| 0.84 | 0.72524 | 0.60126 |
| 0.85 | 0.72282 | 0.60639 |
| 0.86 | 0.72042 | 0.61148 |
| 0.87 | 0.71803 | 0.61654 |
| 0.88 | 0.71566 | 0.62157 |
| 0.89 | 0.71331 | 0.62657 |
| 0.90 | 0.71097 | 0.63153 |
| 0.91 | 0.70865 | 0.63646 |
| 0.92 | 0.70634 | 0.64136 |
| 0.93 | 0.70405 | 0.64623 |
| 0.94 | 0.70177 | 0.65106 |
| 0.95 | 0.69951 | 0.65587 |
| 0.96 | 0.69726 | 0.66064 |
| 0.97 | 0.69503 | 0.66539 |
| 0.98 | 0.69281 | 0.67010 |
| 0.99 | 0.69061 | 0.67479 |
| D/l | K | K1 |
|---|---|---|
| 1.00 | 0.68842 | 0.67945 |
| 1.05 | 0.67770 | 0.70230 |
| 1.10 | 0.66731 | 0.72447 |
| 1.15 | 0.65726 | 0.74600 |
| 1.20 | 0.64753 | 0.76690 |
| 1.25 | 0.63809 | 0.78722 |
| 1.30 | 0.62895 | 0.80697 |
| 1.35 | 0.62009 | 0.82620 |
| 1.40 | 0.61149 | 0.84492 |
| 1.45 | 0.60314 | 0.86316 |
| 1.50 | 0.59505 | 0.88093 |
| 1.55 | 0.58718 | 0.89826 |
| 1.60 | 0.57954 | 0.91518 |
| 1.65 | 0.57212 | 0.93169 |
| 1.70 | 0.56490 | 0.94781 |
| 1.75 | 0.55788 | 0.96357 |
| 1.80 | 0.55106 | 0.97897 |
| 1.85 | 0.54441 | 0.99403 |
| 1.90 | 0.53795 | 1.00877 |
| 1.95 | 0.53165 | 1.02319 |
| 2.00 | 0.52551 | 1.03732 |
| 2.10 | 0.51370 | 1.06471 |
| 2.20 | 0.50247 | 1.09102 |
| 2.30 | 0.49178 | 1.11635 |
| 2.40 | 0.48159 | 1.14075 |
| D/l | K | K1 |
|---|---|---|
| 2.50 | 0.47186 | 1.16428 |
| 2.60 | 0.46257 | 1.18701 |
| 2.70 | 0.45369 | 1.20898 |
| 2.80 | 0.44518 | 1.23024 |
| 2.90 | 0.43702 | 1.25084 |
| 3.00 | 0.42920 | 1.27081 |
| 3.10 | 0.42169 | 1.29018 |
| 3.20 | 0.41447 | 1.30900 |
| 3.30 | 0.40752 | 1.32730 |
| 3.40 | 0.40084 | 1.34509 |
| 3.50 | 0.39440 | 1.36241 |
| 3.60 | 0.38819 | 1.37927 |
| 3.70 | 0.38220 | 1.39571 |
| 3.80 | 0.37642 | 1.41175 |
| 3.90 | 0.37083 | 1.42739 |
| 4.00 | 0.36543 | 1.44267 |
| 4.10 | 0.36021 | 1.45759 |
| 4.20 | 0.35515 | 1.47217 |
| 4.30 | 0.35025 | 1.48643 |
| 4.40 | 0.34550 | 1.50039 |
| 4.50 | 0.34090 | 1.51404 |
| 4.60 | 0.33643 | 1.52741 |
| 4.70 | 0.33210 | 1.54051 |
| 4.80 | 0.32789 | 1.55335 |
| 4.90 | 0.32380 | 1.56593 |
| D/l | K | K1 |
|---|---|---|
| 5.00 | 0.31983 | 1.57828 |
| 5.50 | 0.30150 | 1.63665 |
| 6.00 | 0.28541 | 1.69013 |
| 6.50 | 0.27115 | 1.73947 |
| 7.00 | 0.25841 | 1.78526 |
| 7.50 | 0.24695 | 1.82797 |
| 8.00 | 0.23658 | 1.86798 |
| 8.50 | 0.22715 | 1.90562 |
| 9.00 | 0.21853 | 1.94114 |
| 9.50 | 0.21062 | 1.97478 |
| 10.00 | 0.20332 | 2.00672 |
| 10.50 | 0.19658 | 2.03713 |
| 11.00 | 0.19031 | 2.06613 |
| 11.50 | 0.18448 | 2.09387 |
| 12.00 | 0.17904 | 2.12043 |
| 12.50 | 0.17394 | 2.14593 |
| 13.00 | 0.16916 | 2.17043 |
| 13.50 | 0.16467 | 2.19402 |
| 14.00 | 0.16043 | 2.21676 |
| 14.50 | 0.15643 | 2.23870 |
| 15.00 | 0.15265 | 2.25991 |
| 15.50 | 0.14907 | 2.28043 |
| 16.00 | 0.14567 | 2.30030 |
| 16.50 | 0.14244 | 2.31956 |
| 17.00 | 0.13936 | 2.33825 |
| D/l | K | K1 |
|---|---|---|
| 17.50 | 0.13643 | 2.35640 |
| 18.00 | 0.13363 | 2.37405 |
| 18.50 | 0.13096 | 2.39121 |
| 19.00 | 0.12841 | 2.40792 |
| 19.50 | 0.12596 | 2.42419 |
| 20.00 | 0.12361 | 2.44006 |
| 22.00 | 0.11513 | 2.49980 |
| 24.00 | 0.10784 | 2.55436 |
| 26.00 | 0.10150 | 2.60457 |
| 28.00 | 0.09593 | 2.65106 |
| 30.00 | 0.09100 | 2.69435 |
| 32.00 | 0.08659 | 2.73485 |
| 34.00 | 0.08263 | 2.77290 |
| 36.00 | 0.07905 | 2.80878 |
| 38.00 | 0.07580 | 2.84272 |
| 40.00 | 0.07282 | 2.87493 |
| 50.00 | 0.06110 | 3.01505 |
| 60.00 | 0.05285 | 3.12955 |
| 70.00 | 0.04670 | 3.22638 |
| 80.00 | 0.04192 | 3.31026 |
| 90.00 | 0.03810 | 3.38425 |
| 100.00 | 0.03496 | 3.45044 |
| 200.00 | 0.01969 | 3.88592 |
| 300.00 | 0.01398 | 4.14067 |
| 400.00 | 0.01095 | 4.32143 |
Abaque
Pour les amateurs d'abaques, ce graphe donne \(K\) en fonction dur rapport \(D/l\).
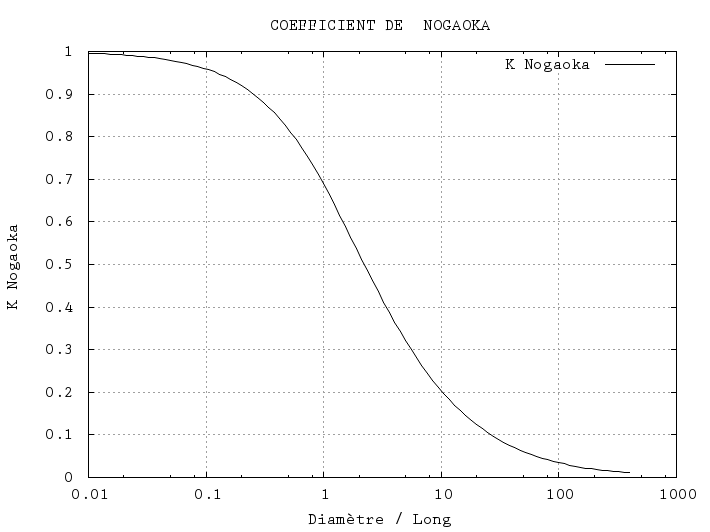

Pour ceux qui n'aime pas les méthodes tabulaires.
$$K = \displaystyle \frac{100}{\displaystyle \pi^2 (4 \frac {D}{l}+11)} \quad \quad (4)$$
fig.3 - Calcul approché de K
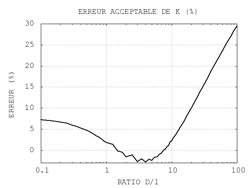
Pour ceux qui n'aiment pas cette approche tabulaire, il est possible d'approcher K par la relation de la fig.3
à condition d'accepter une marge d'erreur évaluée sur la fig.4
Par exemple pour un rapport D/l = 1, on retrouve K = 0.68.
Par exemple pour un rapport D/l = 1, on retrouve K = 0.68.
Une formule empirique pour une bobine massée (multicouches)
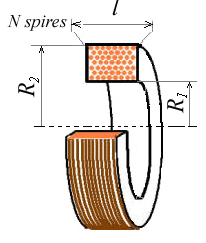
fig.5 Bobine multicouches
Une formule de calcul approché dans le cas d'une bobine massée ou multicouches.
$$\left\{\begin{array}{l} L_{µH}\ :\ \displaystyle \frac{10\pi N^2R_1^2 }{6R_1+9l+10(R_2-R_1)}\\ L\ :\ inductance\ en\ Henry\\ N\ :\ nombre\ total\ de\ spire\\ R_1\ :\ Rayon\ du\ mandrin\ (m)\\ R_2\ :\ Rayon\ ext\acute{e}rieur\ du\ bobinage\ (m)\\ l\ :\ longueur\ du\ bobinage\ (m))\\ R_2-R_1\ :\ est\ l'\acute{e}paisseur\ du\ bobinage \end{array}\right. $$
$$\left\{\begin{array}{l} L_{µH}\ :\ \displaystyle \frac{10\pi N^2R_1^2 }{6R_1+9l+10(R_2-R_1)}\\ L\ :\ inductance\ en\ Henry\\ N\ :\ nombre\ total\ de\ spire\\ R_1\ :\ Rayon\ du\ mandrin\ (m)\\ R_2\ :\ Rayon\ ext\acute{e}rieur\ du\ bobinage\ (m)\\ l\ :\ longueur\ du\ bobinage\ (m))\\ R_2-R_1\ :\ est\ l'\acute{e}paisseur\ du\ bobinage \end{array}\right. $$
Une formule empirique pour une bobine plate spirale
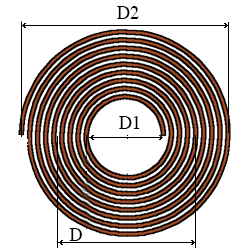
fig.6 Bobine multicouches
$$
\left\{\begin{array}{l}
L(µH)=K2_{(C/D)} \displaystyle \frac {N^2 D}{2000} \\
D =\displaystyle \frac {D_2 + D_1}{2} \\
C=\displaystyle \frac {D_2 - D_1}{2} \\
N \quad spires
\end{array}\right.
$$
Exemple :
Calculons l'inductance L d'une bobine plate de 100 spires de dimensions :
L'inductance L sera 25,418 x 1002 x 3/2000 = ≈ 381 µH
- diamètre extérieur D2 = 4 cm
- diamètre intérieur D1 = 2 cm
L'inductance L sera 25,418 x 1002 x 3/2000 = ≈ 381 µH
| C/D | K2 |
|---|---|
| 0.00 | 7.11200 |
| 0.01 | 69.00800 |
| 0.02 | 60.29900 |
| 0.03 | 55.20600 |
| 0.04 | 51.59400 |
| 0.05 | 48.79300 |
| 0.06 | 46.50700 |
| 0.07 | 44.57400 |
| 0.08 | 42.90200 |
| 0.09 | 41.42800 |
| 0.10 | 40.11100 |
| 0.11 | 38.92000 |
| 0.12 | 37.83500 |
| 0.13 | 36.83800 |
| 0.14 | 35.91600 |
| 0.15 | 35.05800 |
| 0.16 | 34.25800 |
| 0.17 | 33.50700 |
| 0.18 | 32.80000 |
| 0.19 | 32.13200 |
| 0.20 | 31.50000 |
| 0.21 | 30.90000 |
| 0.22 | 30.32900 |
| 0.23 | 29.78500 |
| 0.24 | 29.26500 |
| C/D | K2 |
|---|---|
| 0.25 | 28.76700 |
| 0.26 | 28.29000 |
| 0.27 | 27.83200 |
| 0.28 | 27.39200 |
| 0.29 | 26.96800 |
| 0.30 | 26.56000 |
| 0.31 | 26.16600 |
| 0.32 | 25.78600 |
| 0.33 | 25.41800 |
| 0.34 | 25.06300 |
| 0.35 | 24.71900 |
| 0.36 | 24.38600 |
| 0.37 | 24.06300 |
| 0.38 | 23.75000 |
| 0.39 | 23.44600 |
| 0.40 | 23.15000 |
| 0.41 | 22.86300 |
| 0.42 | 22.58400 |
| 0.43 | 22.31300 |
| 0.44 | 22.04900 |
| 0.45 | 21.79200 |
| 0.46 | 21.54100 |
| 0.47 | 21.29700 |
| 0.48 | 21.05900 |
| 0.49 | 20.82700 |
| C/D | K2 |
|---|---|
| 0.50 | 20.60100 |
| 0.51 | 20.38100 |
| 0.52 | 20.16500 |
| 0.53 | 19.95500 |
| 0.54 | 19.75000 |
| 0.55 | 19.55000 |
| 0.56 | 19.35400 |
| 0.57 | 19.16200 |
| 0.58 | 18.97600 |
| 0.59 | 18.79300 |
| 0.60 | 18.61400 |
| 0.61 | 18.44000 |
| 0.62 | 18.26900 |
| 0.63 | 18.10200 |
| 0.64 | 17.93900 |
| 0.65 | 17.77900 |
| 0.66 | 17.62300 |
| 0.67 | 17.47000 |
| 0.68 | 17.32100 |
| 0.69 | 17.17400 |
| 0.70 | 17.03100 |
| 0.71 | 16.89100 |
| 0.72 | 16.75400 |
| 0.73 | 16.62000 |
| 0.74 | 16.48900 |
| C/D | K2 |
|---|---|
| 0.75 | 16.36000 |
| 0.76 | 16.23500 |
| 0.77 | 16.11200 |
| 0.78 | 15.99200 |
| 0.79 | 15.87400 |
| 0.80 | 15.75900 |
| 0.81 | 15.64600 |
| 0.82 | 15.53600 |
| 0.83 | 15.42800 |
| 0.84 | 15.32300 |
| 0.85 | 15.22000 |
| 0.86 | 15.12000 |
| 0.87 | 15.02100 |
| 0.88 | 14.92500 |
| 0.89 | 14.83100 |
| 0.90 | 14.74000 |
| 0.91 | 14.65000 |
| 0.92 | 14.56300 |
| 0.93 | 14.47800 |
| 0.94 | 14.39400 |
| 0.95 | 14.31300 |
| 0.96 | 14.23400 |
| 0.97 | 14.15800 |
| 0.98 | 14.08300 |
| 0.99 | 14.01000 |
Sources et références
[1] Frederick W. GROVER, "Inductance calculation", Dover Publications, Inc., New York 1946, 2001
[2] Paul BERCHE, "Pratique et théorie de la TSF", Librairie de la Radio, Paris, 1937, revue par Roger RAFFIN, 1958.
[4] F. E. TERMAN, "Radio Engineer's Handbook", McGraw-Hill, New York, 1943.